1836. Alignment

In the army, a platoon is composed by n soldiers. During the morning inspection, the soldiers are aligned in a straight line in front of the captain. The captain is not satisfied with the way his soldiers are aligned; it is true that the soldiers are aligned in order by their code number: 1 , 2 , 3 , . . . , n , but they are not aligned by their height. The captain asks some soldiers to get out of the line, as the soldiers that remain in the line, without changing their places, but getting closer, to form a new line, where each soldier can see by looking lengthwise the line at least one of the line's extremity (left or right). A soldier see an extremity if there isn't any soldiers with a higher or equal height than his height between him and that extremity.

Write a program that, knowing the height of each soldier, determines the minimum number of soldiers which have to get out of line.

Input. On the first line of the input is written the number of the soldiers n. On the second line is written a series of n floating numbers with at most 5 digits precision and separated by a space character. The k-th number from this line represents the height of the soldier who has the code k (1 ≤ k ≤ n).

There are some restrictions:

• 2 ≤ n ≤ 1000

• the height are floating numbers from the interval [0.5, 2.5]

Output. The only line of output will contain the number of the soldiers who have to get out of the line.

Sample input	Sample output
8 1.86 1.86 1.30621 2 1.4 1 1.97 2.2	4

РЕШЕНИЕ

наибольшая возрастающая подпоследовательность

Анализ алгоритма

Пусть имеется последовательность s₁, s₂, …, s_n. Для каждого элемента s_i (1 ≤ i ≤ n) найдем длину НВП, которая заканчивается в x_i. Это значение сохраним в Left[i].

Аналогично заполним массив Right[i], вычисляя НВП входной последовательности справа налево.

Остается перебрать все пары индексов (i, j) (1 ≤ i < j ≤ n) и найти максимальное значение выражения Left[i] + Right[j]. Слева от s_i достаточно убрать i – Left[i] солдат так чтобы i-ый солдат мог смотреть влево в бесконечность. Справа от s_j достаточно убрать n – j + 1 – Right[j] солдат так, чтобы j-ый солдат мог смотреть вправо в бесконечность.

В строю останется Left[i] + Right[j] солдат, следовательно из строя следует убрать n - Left[i] – Right[j] солдат.

Пример

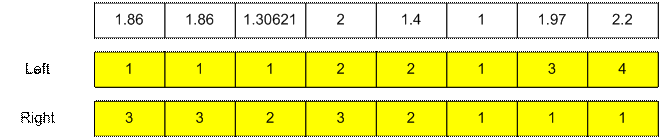
Максимальная искомая сумма равна например Left[4] + Right[5] = 2 + 2 = 4. Тогда в строю останутся солдаты со следующими высотами:

Максимальная искомая сумма может равняться и Left[7] + Right[8] = 3 + 1 = 4. Тогда в строю останутся следующщие солдаты:

Реализация алгоритма

#include <cstdio>

#include <algorithm>

#define MAX 1001

using namespace std;

double x[MAX], lis[MAX];

int Left[MAX], Right[MAX];

int i, j, n, len, pos, ans;

int main(void)

{

scanf("%d",&n);

for(i = 0; i < n; i++) scanf("%lf",&x[i]);

for (len = i = 0; i < n; i++)

{

pos = lower_bound(lis,lis+len,x[i]) - lis;

lis[pos] = x[i];

Left[i] = pos + 1;

if (pos == len) len++;

}

for (len = 0, i = n - 1; i >= 0; i--)

{

pos = lower_bound(lis,lis+len,x[i]) - lis;

lis[pos] = x[i];

Right[i] = pos + 1;

if (pos == len) len++;

}

for (i = 0; i < n; i++)

for (j = i + 1; j < n; j++)

if (Left[i] + Right[j] > ans) ans = Left[i] + Right[j];

printf("%d\n",n - ans);

return 0;

}